
- #Perimeter of a rectangle calculator how to#
- #Perimeter of a rectangle calculator code#
Step 2: Now click the button Calculate to get the perimeter value.
#Perimeter of a rectangle calculator how to#
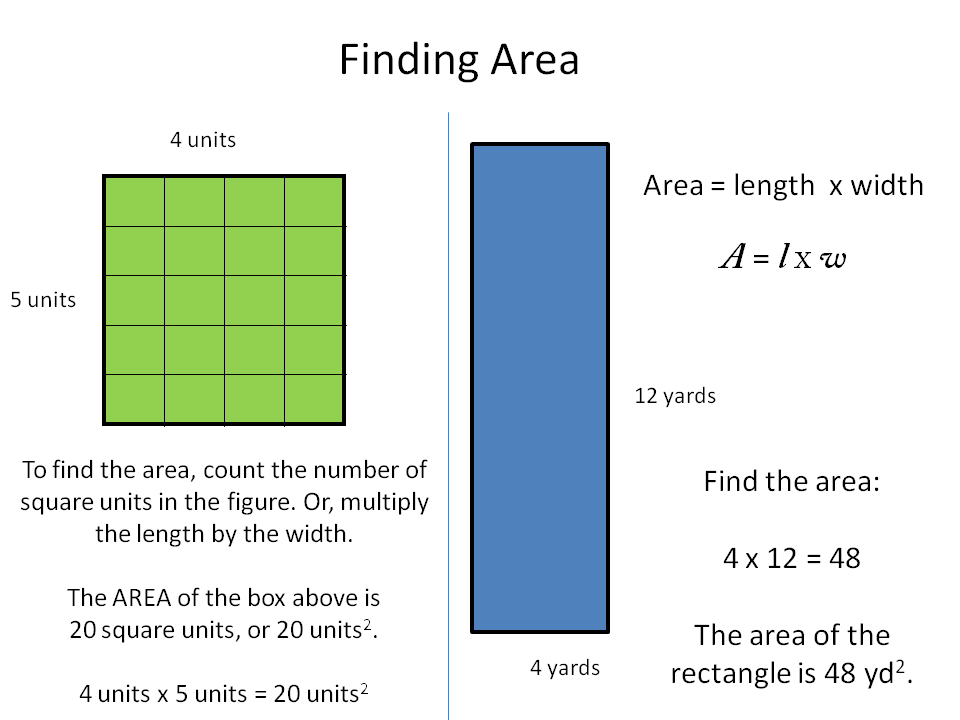
Here we read the value of length and width and calculate the perimeter of the Rectangle using the below formula, and then print the result on the console screen. How to Use the Perimeter of a Triangle Calculator The procedure to use the perimeter of a triangle calculator is as follows: Step 1: Enter the side values of a triangle in the input field. The Main() method is the entry point for the program. Perimeter of a rectangle 2 (Length + Width) units. Here, we created a class Rectangle that contains a method Main(). Program to calculate the perimeter of the //rectangle in C# using System class Rectangle The given program is compiled and executed successfully on Microsoft Visual Studio. From the width and height shown, calculate the perimeter and verify your result matches.
#Perimeter of a rectangle calculator code#
The source code to calculate the perimeter of the Rectangle is given below. In the figure above, drag any orange dot to resize the rectangle. Here, we will calculate the perimeter of the Rectangle using the below formula.
Perimeter of Circular Shaped Area: Computes the length of the fence perimeter in a circular shaped area base on the radius (half diameter) of the area.Here, we are going to learn how to calculate the perimeter of Rectangle in C#?. What is the width Solution: Lets plug the given dimensions into the formula, then isolate w to. Make sure both are in the same unit, or convert one of them as necessary. Problem 2: A rectangle has a perimeter of 15 and a length of 5. This is useful in ensuring that your area has square corners. Perimeter of a rectangle The formula for the perimeter of a rectangle is (width + height) x 2, as seen in the figure below: You need two measurements for a rectangle - width and length. Diagonal of the Rectanglecomputes the diagonal measurement of a rectangular area. Perimeter of a Rectangular Shaped Area computes the length of a fence perimeter in a rectangular shaped area base on the length (l) and width (w) of the area. Labor Cost for Posts : Computes the approximate cost of labor in digging and setting fence posts based on the length of the fence, uniform distance between posts, method of digging (by hand, power auger) and the hourly labor pay rate (DPH). Wire Fence Cost Estimate Computes the materials and costs of a high tension wire fence. Wire Fence Materials: Computes the materials needed for a high tension fence. Wood Fence Cost Estimate : Computes material costs for post and rail fence based on the number of posts and rails (above) and unit cost pricing. Number of Posts and Rails: Computes the number of fence posts and rails needed for a length of wood fencing. The formula for the perimeter of a rectangle is: Compute the Diagonal in a Rectangle Fenced Area A rectangle with a length of 10 and a width of 5 would have a perimeter of 30 given by the calculator. Compute the Area of a Four-sided Fenced Area. However, these can be automatically converted to compatible units via the pull-down menu. How to Use the Perimeter of a Rectangle Calculator Step 1: Enter the value of length and width of the rectangle. Example 2: Calculate the length of a rectangle whose width and perimeter are 10 cm and 48 cm, respectively. Thus, the perimeter of the rectangle is 74 feet. 2 × (25 + 12) Substitute values of length and width. 
It also returns the area in square feet and acres, and the length of the diagonal in feet. Solution : Perimeter of rectangle (P) 2 (l + w) Formula for perimeter of rectangle. Rectangle Field Perimeter (P): The calculator returns the perimeter in feet. INSTRUCTIONS: Choose units and enter the follow: Finding the perimeter of a rectangle is as easy as adding up all its side lengths.

The Perimeter of a Rectangle Fence calculator computes the length of the perimeter (P) of a rectangle field or area based on the dimensions (length and width). The Rectangle Formulas There's no mystery to rectangle calculation, most of it being based in elementary math: Perimeter (X 2) + (Y 2) Area X Y Diagonal ( (X 2) + (Y 2)) Circumcircle radius Diagonal / 2 The angle part is the only tricky one, requiring we take the inverse of the standard trigonometric function tangent.








 0 kommentar(er)
0 kommentar(er)
